자료구조 - 트리(tree)

트리(tree) : Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조

                          → 트리 중 이진 트리(Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨

 

1-1 알아둘 용어 :

• Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
• Root Node: 트리 맨 위에 있는 노드
• Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
• Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
• Child Node: 어떤 노드의 상위 레벨에 연결된 노드
• Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
• Sibling (Brother Node): 동일한 Parent Node를 가진 노드
• Depth: 트리에서 Node가 가질 수 있는 최대 Level

□ 이진 트리와 이진 탐색 트리(Binary Search Tree)

• 이진 트리: 노드의 최대 Branch가 2인 트리
• 이진 탐색 트리 (Binary Search Tree, BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
  • 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음

출처:  https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node

• 주요 용도: 데이터 검색(탐색)
• 장점: 탐색 속도를 개선할 수 있음

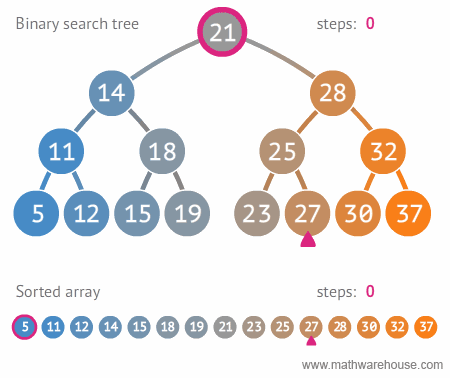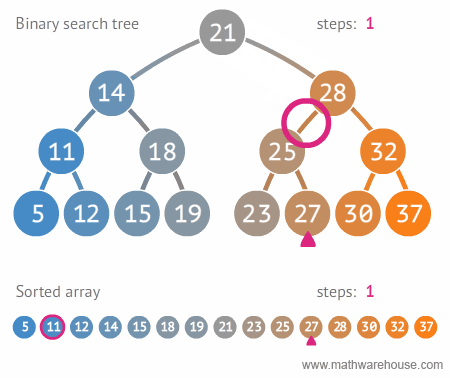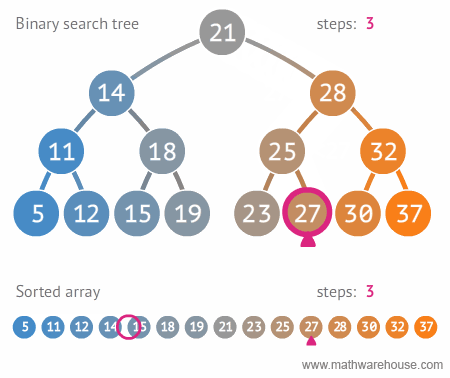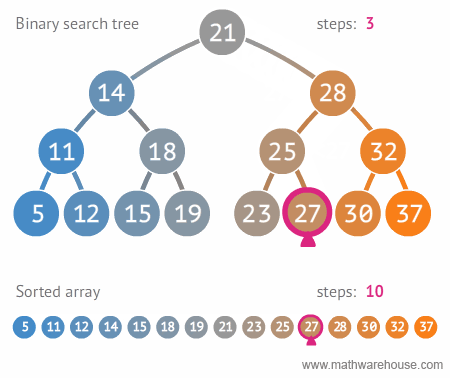
□ 이진 트리와 정열된 배열간의 탐색 비교

출처:  https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node

□ 노드 클래스 만들기

※ __init__ 이란?

__init__은 파이썬 클래스에서 특별한 메서드로, 초기화를 담당합니다.

이 메서드는 클래스가 인스턴스화될 때 자동으로 호출되며,

인스턴스의 속성을 초기화하거나 다른 초기화 작업을 수행하는 데 사용됩니다.

□ 이진 탐색 트리에 데이터 넣기 및  탐색

이진트리 입력 및 탐색출력

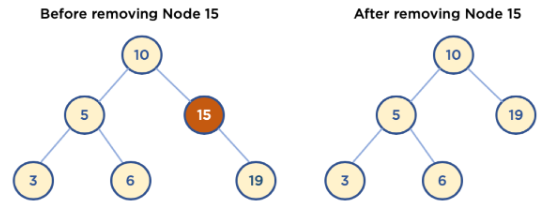
□ 이진 탐색 트리 삭제

※ 매우 복잡함, 경우를 나누어서 이해하는것이 좋음

 

① Leaf Node 삭제

• Leaf Node: Child Node 가 없는 Node
• 삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않도록 한다.

② Child Node가 하나인 Node 삭제

• 삭제할 Node의 Parent Node가 삭제할 Node의 Child Node를 가리키도록 한다.

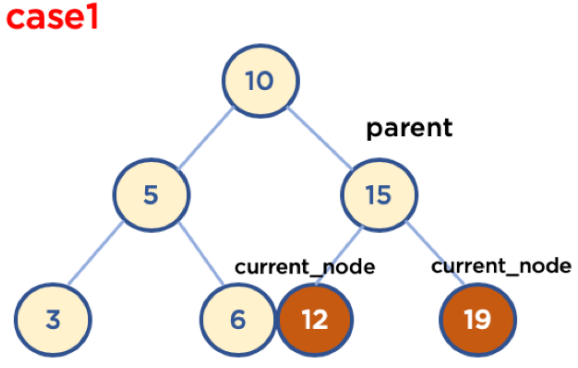
③ Child Node가 두개인 Node 삭제 

1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
2. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.

④ 삭제할 Node의 오른쪽 자식중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 할 경우

• 삭제할 Node의 오른쪽 자식 선택
• 오른쪽 자식의 가장 왼쪽에 있는 Node를 선택
• 해당 Node를 삭제할 Node의 Parent Node의 왼쪽 Branch가 가리키게 함
• 해당 Node의 왼쪽 Branch가 삭제할 Node의 왼쪽 Child Node를 가리키게 함
• 해당 Node의 오른쪽 Branch가 삭제할 Node의 오른쪽 Child Node를 가리키게 함
• 만약 해당 Node가 오른쪽 Child Node를 가지고 있었을 경우에는, 
  해당 Node의 본래 Parent Node의 왼쪽 Branch가 해당 오른쪽 Child Node를 가리키게 함

□ 이진 탐색 트리 삭제 코드 구현과 분석

삭제할 Node 탐색

 

 

Case1: 삭제할 Node가 Leaf Node인 경우

Case2: 삭제할 Node가 Child Node를 한 개 가지고 있을 경우

Case3-1: 삭제할 Node가 Child Node를 두 개 가지고 있을 경우(삭제할 Node가 Parent Node 왼쪽에 있을 때)

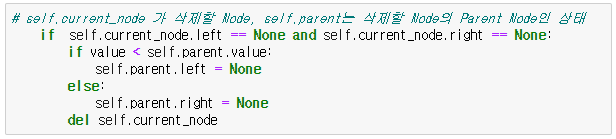
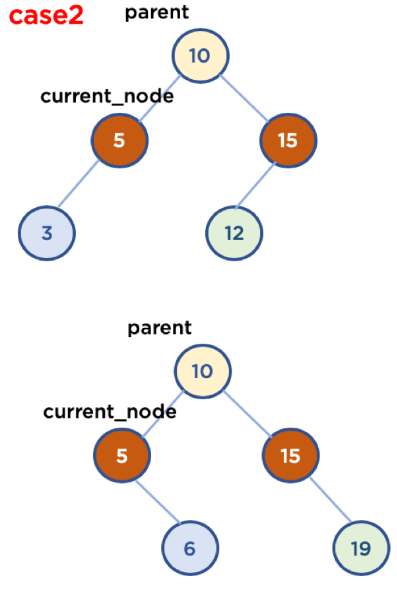
• 기본 사용 가능 전략
  1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
  2. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
• 기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현하기로 함
  • 경우의 수가 또다시 두가지가 있음
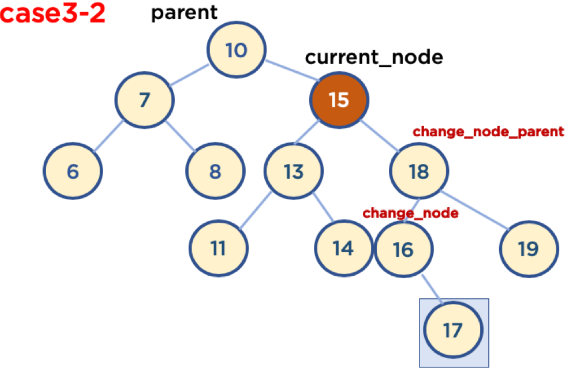
    • Case3-1-1: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
    • Case3-1-2: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때
      • 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문임

Case3-2-2: 삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때

 

□ 이진 탐색 트리의 시간 복잡도와 단점

• depth (트리의 높이) 를 h라고 표기한다면, O(h)
• n개의 노드를 가진다면, ℎ=𝑙𝑜𝑔2𝑛 에 가까우므로, 시간 복잡도는 O(𝑙𝑜𝑔𝑛)
  • 참고: 빅오 표기법에서 𝑙𝑜𝑔𝑛에서의 log의 밑은 10이 아니라, 2입니다.
    • 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미.
      즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함

출처:  https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node

• 평균 시간 복잡도는 O(𝑙𝑜𝑔𝑛)이지만,
  • 이는 트리가 균형잡혀 있을 때의 평균 시간복잡도이며,
• 다음 예와 같이 구성되어 있을 경우, 최악의 경우는 링크드 리스트등과 동일한 성능을 보여줌 ( O(𝑛) )